Amazon
Friday, 17 December 2021
TYPES OF PROFITABILITY SAMPLING
8 Important Types of Probability Sampling
The eight important types of probability sampling used for conducting social research. The types are: 1. Simple Random Sampling 2. Systematic Sampling 3. Stratified Random Sampling 4. Proportionate Stratified Sampling 5. Disproportionate Stratified Sampling 6. Optimum Allocation Sample 7. Cluster sampling 8. Multi-Phase Sampling.
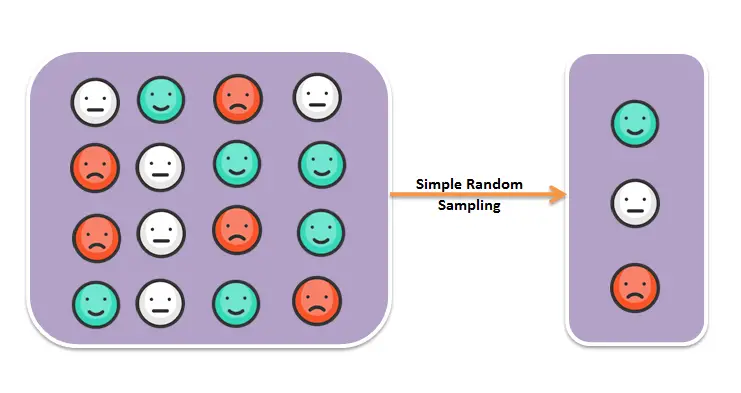
Type # 1. Simple Random Sampling:
A simple random sample is selected by a process that not only gives to each element in the population an equal chance of being included in the sample but also makes the selection of every possible combination of cases in the desired sample size, equally likely. Suppose, for example, that one has a population of six children, viz., A, B, C, D, E and F.
There will be the following possible combinations of cases, each having two elements from this population, viz., AB, AC, AD, AE, AF, BC, BD, BE, BF, CD, CE, EF, DE, DF, and EF, i.e., in all 15 combinations.
If we write each combination on equal sized cards, put the cards in a basket, mix them thoroughly and let a blindfolded person pick one, each of the cards will be afforded the same chance of being selected/included in the sample.
The two cases (the pair) written on the card picked up by the blind-folded person thus, will constitute the desired simple random sample. If one wishes to select simple random samples of three cases from the above population of six cases, the possible samples, each of three cases, will be, ABC, ABD, ABE, ABF, ACD, ACE, ACF, ADE, ADF, BCD, BCE, BCF, BDE, BDF, BEF, CDE, CDF, CEF, and DEF, i.e., 20 combinations in all.
Each of these combinations will have an equal chance of selection in the sample. Using the same method, one can select a simple random sample of four cases from this population.
In principle, one can use this method for selecting random samples of any size from a population. But in practice, it would become a very cumbersome and in certain cases an impossible task to list out all possible combinations of the desired number of cases. The very same result may be obtained by selecting individual elements, one by one, using the above method (lottery) or by using a book of random numbers.
The book of tables comprising list of random numbers is named after Tippet who was first to translate the concept of randomness into a book of random numbers.
This book is prepared by a very complicated procedure in such a manner that the numbers do not show any evidence of systematic order, that is, no one can estimate the number following, on the basis of the preceding number and vice-versa. Let us discuss the two methods of drawing a simple random sample.
Lottery Method:
This method involves the following steps:
(a) Each member or item in the ‘population’ is assigned a unique number. That is, no two members have the same number,
(b) Each number is noted on a separate card or a chip. Each chip or card should be similar to all the others with respect to weight, size and shape, etc.,
(c) The cards or chips are placed in a bowl and mixed thoroughly,
(d) A blind-folded person is asked to pick up any chip or card from the bowl.
Under these circumstances, the probability of drawing any one card can be expected to be the same as the probability of drawing any other card. Since each card represents a member of the population, the probability of selecting each would be exactly the same.
If after selecting a card (chip) it was replaced in the bowl and the contents again thoroughly mixed, each chip would have an equal probability of being selected on the second, fourth, or nth drawing. Such a procedure would ultimately yield a simple random sample.
Selecting Sample with the Help of Random Numbers:
We have already said what random numbers are. These numbers help to avoid any bias (unequal chances) to items comprising a population, of being included in the sample in selecting the sample.
These random numbers are so prepared that they fulfill the mathematical criterion of complete randomness. Any standard book on statistics contains a few pages of random numbers. These numbers are generally listed in columns on consecutive pages.
The use of the tables of random numbers involves the following steps:
(a) Each member of the population is assigned a unique number. For example, one member may have the number 77 and another 83, etc.
(b) The table of random numbers is entered at some random point (with a blind mark on any page of the book of tables) and the cases whose numbers come up as one moves from this point down the column are included in the sample until the desired number of cases is obtained.
Suppose our population consists of five hundred elements and we wish to draw fifty cases as a sample. Suppose we use the last three digits in each number of five digits (since the universe size is 500, i.e., three-digital).
We proceed down the column starting with 42827; but since we have decided to use only three digits (say the last three), we start with 827 (ignoring the first two digits). We now note each number less than 501 (since the population is of 500).
The sample would be taken to consist of the elements of the population bearing the numbers corresponding to those chosen. We stop after we have selected 50 (the size decided by us) elements. On the basis of the above section of the table, we shall be choosing 12 numbers corresponding to those chosen. We shall choose 12 cases corresponding to the numbers 237, 225, 280, 184, 203, 190, 213, 027, 336, 281, 288, 251.
Characteristics of Simple Random Sample:
We shall start by considering one very important property of the simple random samples; this being, that larger the size of the sample, the more likely it is that its mean (average value) will be
close to the ‘population’ mean, i.e., the true value. Let us illustrate this property by supposing a population comprising six members (children).
Let the ages of these children be respectively: A=2 years, B=3 years, C=4 years, D=6 years, E=9 years and F=12 years. Let us draw random samples of one, two, three four and five members each from this population and see how in each case, the sample means (averages) behave with reference to the true ‘population’ mean (i.e., 2+3+4+6+9+12 = 36/ 6 = 6). Table following illustrates the behaviour of the sample means as associated with the size of the sample.
Table showing the possible samples of one, two, three, four and five elements (children, from the population of six children of ages 2, 3, 4, 6, 9 and 12 years respectively):
In the given table, all possible random samples of various sizes (i.e., 1, 2, 3, 4 and 5) and their corresponding means are shown. The true (population) mean is 6 years. This mean can of course be calculated by adding up the mean-values of the total combinations of the elements in the population for any given sample size.
In the table we see, for example, that for the sample size of three elements there are 20 possible combinations of elements, each combination having an equal chance of being selected as a sample according to the principle of probability.
Adding up the mean-values of these possible combinations shown in the table, we get the total score of 120. The mean will be 120 ÷20 = 6, which is also, of course, the population mean. This holds good for other columns too.
Let us now examine the table carefully. We shall find that for samples of one element each (column A) there is only one mean-value which does not deviate by more than 1 unit from the true population mean of 6 years. That is, all others, viz., 2, 3, 4, 9 and 12, deviate by more than one unit from the population mean, i.e., 6. As we increase the size of the sample, e.g., in column B, where the sample size is 2, we find a greater proportion of means (averages) that do not deviate from the population mean by more than 1 unit.
The above table shows that for the sample of two, there are 15 possible combinations and hence 15 possible means. Out of these 15 means there are 5 means which do not deviate from the population mean by more than 1 unit.
That is, there are 33% of the sample means which are close to the population mean within +1 and -1 units. In column C of the table, we see that there are 20 possible combinations of elements for the sample-size of three elements, each.
From out of the 20 possible sample-means, we find that 10, i.e., 50% do not deviate from the population mean by more than 1 unit. For the sample size of four elements, there are 67% of means which are within the range of +1 and -1 unit from the true (population) mean.
Lastly, for the sample size of five elements, there are much more, i.e., 83% of such means or estimates. The lesson surfacing out of our observations is quite clear, viz., the larger the sample, the more likely it is that its mean will be close to the population mean.
This is the same thing as saying that the dispersion of estimates (means) decreases as the sample size increases. We can clearly see this in the above table. For the sample size of one (column A) the range of means is the largest, i.e., between 2 and 12 = 10. For the sample size of two the range is between 2.5 and 10.5 = 8.
For the sample size of three, four and five, the range of variability of means is respectively 3 to 9 = 6, 3.8 to 7.8 = 4 and 4.8 to 6.8 = 2. It will also be seen from the table that the more a sample mean differs from population-mean the less frequently it is likely to occur.
We can represent this phenomenon relating to simple random sampling clearly with the help of a series of curves showing the relationship between variability of estimates and the size of sample. Let us consider a big population of residents. One can imagine that their ages will range between below 1 year (at the least) and above 80 years (at the most).
The normal and reasonable expectation would be that there are lesser cases as one approaches the extremes and that the number of cases goes on increasing progressively and symmetrically as we move away from these extremes.
The mean-age of the population is, let us say, 40 years. Such a distribution of residents can be represented by a curve known as the normal or bell-shaped curve (A in the diagram following). Let us now suppose that we take from this population various random samples of different sizes, e.g., 10,100 and 10,000. For any of the sample-size we shall get a very large number of samples from the population.
Each of these samples will give us a particular estimate of the population mean. Some of these means will be over-estimates and some under-estimates of the population characteristic (mean or average age). Some means will be very close to it, quite a few rather far.
If we plot such sample means for a particular sample-size and join these points we shall in each case, get a normal curve. Different normal curves will thus represent the values of sample-means for samples of different sizes.
Distribution of Mean-Values
The above diagram approximates a picture of how the sample-means would behave relative to the size of the sample. The curve A represents the locations of ages of single individuals. The estimated means of samples of 10 individuals, each, from the curve B that shows quite a wide dispersion from true population-mean 40 years).
The means of samples of 100 individuals each, form a normal curve C which shows much lesser deviation from the population mean. Finally, the means of the samples of 10,000 from a curve that very nearly approximates the vertical line corresponding to the population mean. The deviation of the values representing curve D from the population mean would be negligible, as is quite evident from the diagram.
It can also be discerned very easily from the above figure that for samples of any given size, the most likely sample-mean is the population-mean. The next most likely are the mean values close to the population mean.
Thus, we may conclude that the more a sample mean deviates from the population-mean, the less likely it is to occur. And lastly, we also see what we have already said about the behaviour of the samples, namely, the larger the sample the more likely it is that its mean will be close to the population-mean.
It is this kind of behaviour on the part of the simple random (probability) samples with respect to the mean as well as to proportions and other types of statistics, that makes it possible for us to estimate not only the population-characteristic (e.g., the mean) but also the likelihood that the sample would differ from the true population value by some given amount.
One typical features of the simple random sampling is that when the population is large compared to the sample size (e.g., more than, say, ten times as large), the variabilities of sampling distributions are influenced more by the absolute number of cases in the sample than by the proportion of the population that the sample includes.
In other words, the magnitude of the errors likely to arise consequent upon sampling, depends more upon the absolute size of the sample rather than the proportion it bears with the population, that is, on how big or how small a part it is of the population.
The larger the size of the random sample, the greater the probability that it will give a reasonably good estimate of the population-characteristic regardless of its proportion compared to the population.
Thus, the estimation of a popular vote at a national poll, within the limits of a tolerable margin of error, would not require a substantially larger sample than the one that would be required for an estimation of population vote in a particular province where poll outcome is in doubt.
To elaborate the point, a sample of 500 (100% sample) will give perfect accuracy if a community had only 500 residents. A sample of 500 will give slightly greater accuracy for a township of 1000 residents than for a city of 10,000 residents. But beyond the point at which the sample is a large portion of the ‘universe’ there is no appreciable difference in accuracy with the increases in the size of the ‘universe.’
For any given level of accuracy, identical sample sizes would give same level of accuracy for communities of different population, e.g., ranging from 10,000 to 10 millions. The ratio of the sample- size to the populations of these communities means nothing, although this seems to be important if we proceed by intuition.
Type # 2. Systematic Sampling:
Suppose this frame consists of 1,000 members each with a unique number, i.e., from 1 to 1,000. Let us say, we want to select a sample of 100. We may start by selecting any number between 1 to 10 (both included). Suppose we make a random selection by entering the list and get 7.
We then proceed to select members; starting from 7, with a regular interval of 10. The selected to select members: starting from with a regular interval of 10. The selected sample would thus consist of elements bearing Nos. 7, 17, 27, 37, 47, … 977, 987, 997. These elements together would constitute a systematic sample.
It should be remembered that a systematic sample may be deemed to be a probability sample only if the first case (e.g., 7) has been selected randomly and then every, tenth case from the frame was selected thereafter.
If the first case is not selected randomly, the resulting sample will not be a probability sample since, in the nature of the case, most of the cases which are not at a distance of ten from the initially chosen number will have a Zero (0) probability of being included in the sample.
It should be noted that in the systematic sampling when the first case is drawn randomly, there is, in advance, no limitation on the chances of any given case to be included in the sample. But once the first case is selected, the chances of subsequent cases are decisively affected or altered. In the above example, the cases other than 17, 27, 37, 47… etc., have no chance of being included in the sample.
This means that systematic sampling plan does not afford all possible combinations of cases, the same chance of being included in the sample.
Thus, the results may be quite deceptive if the cases in the list are arranged in some cyclical order or if the population is not thoroughly mixed with respect to the characteristics under study (say, income or hours of study), i.e., in a way that each of the ten members had an equal chance of getting chosen.
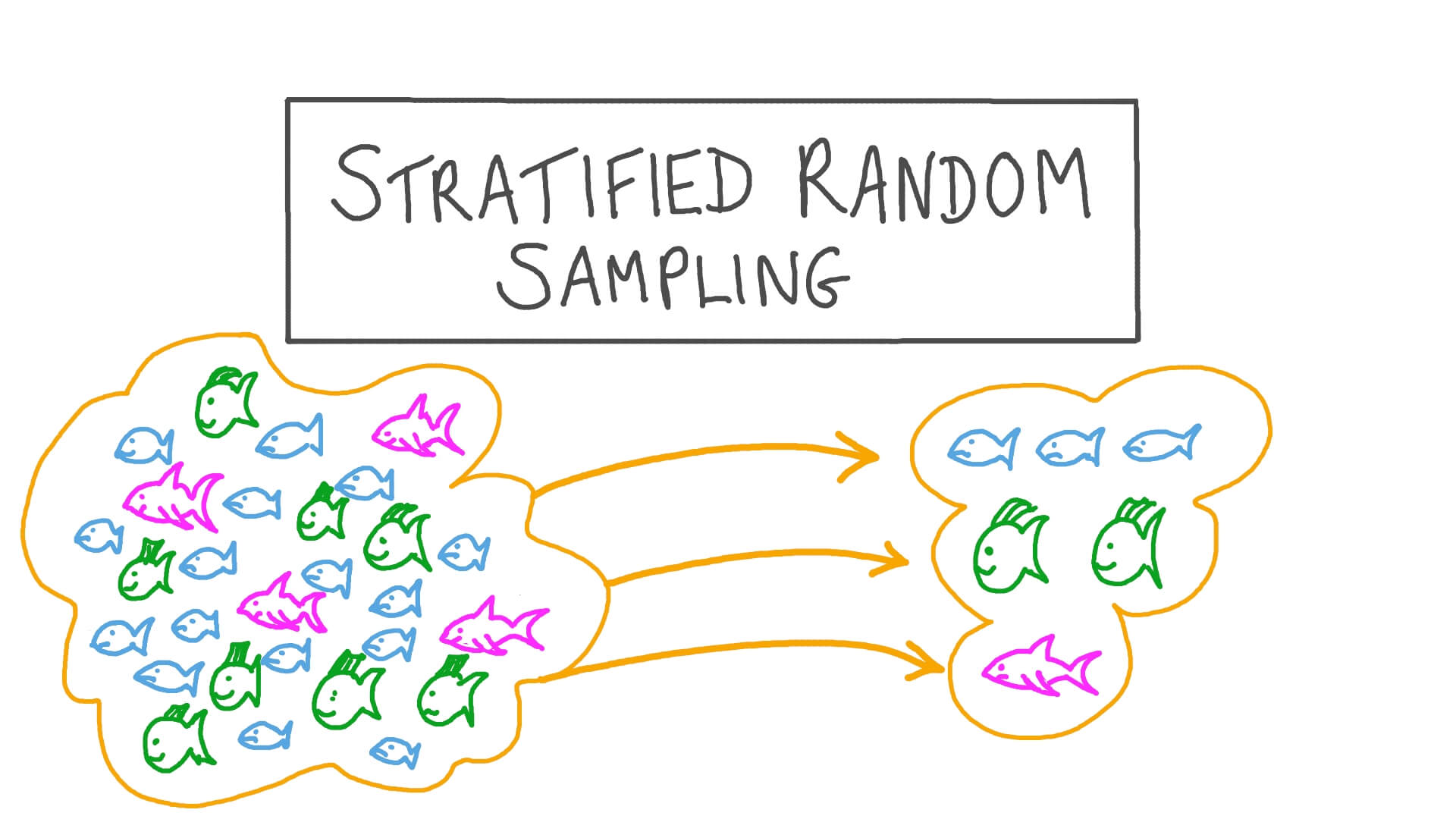
Type # 3. Stratified Random Sampling:
In stratified random sampling, a simple random sample is taken from each of the strata and such sub-samples are brought together to form the total sample.
In general, stratification of the universe for the purpose of sampling contributes to the efficiency of sampling if it establishes classes, that is, if it can divide the population into classes of members or elements that are internally comparatively homogeneous and relative to one another, heterogeneous, with respect to the characteristics being studied. Let us suppose that age and sex are two potential bases of stratification.
Now, should we find that stratification on the basis of sex (male / female) yields two strata which differ markedly from each other in respect of scores on other pertinent characteristics under study while on the other hand, age as a basis of stratification does not yield strata which are substantially different from one another in terms of the scores on the other significant characteristics, then it will be advisable to stratify the population on the basis of sex rather than age.
In other words, the criterion of sex will be more effective basis of stratification in this case. It is quite possible that the process of breaking the population down into strata that are internally homogeneous and relatively heterogeneous in respect of certain relevant characteristics is prohibitively costly.
In such a situation, the researcher may choose to select a large simple random sample and make up for the high cost by increasing (through a large-sized simple random sample) the total size of the sample and avoiding hazards attendant upon stratification.
It should be clearly understood that stratification has hardly anything to do with making the sample a replica of the population.
In fact, the issues involved in the decision whether stratification is to be effected are primarily related to the anticipated homogeneity of the defined strata with respect to the characteristics under study and the comparative costs of different methods of achieving precision. Stratified random sampling like the simple random sampling, involves representative sampling plans.
We now turn to discuss the major forms or stratified sampling. The number of cases selected within each stratum may be proportionate to the strength of the stratum or disproportionate thereto.
The number of cases may be the same from stratum to stratum or vary from one stratum to another depending upon the sampling plan. We shall now consider very briefly these two forms, i.e., proportionate and the disproportionate stratified samples.
Type # 4. Proportionate Stratified Sampling:
In proportionate sampling, cases are drawn from each stratum in the same proportion as they occur in the universe. Suppose we know that 60% of the ‘population’ is male and 40% of it is female. Proportionate stratified sampling with reference to this ‘population’, would involve drawing a sample in a manner that this same division among sexes is reflected, i.e., 60:40, in the sample.
If the systematic sampling procedure is employed in a study, the basis on which the list is made determines whether or not the resulting sample is a proportionate stratified sample. For example, if every 7th name is selected in a regular sequence from a list of alphabetically arranged names, the resulting sample should contain approximately 1/7th of the names beginning with each letter of the alphabet.
The resulting sample in this case would be a proportionate stratified alphabetical sample. Of course, if the alphabetical arrangement is completely unrelated and irrelevant to the problem being studied, the sample might be considered a random sample with certain limitations typical of the systematic samples discussed above.
Various reasons may be adduced for sampling the various strata in unequal or dissimilar proportions. Sometimes, it is necessary to increase the proportion sampled from strata having a small number of cases in order to have a guarantee that these strata come to be sampled at all.
For example, if one were planning a study of retail sales of clothing’s in a certain city at a given point of time, a simple random sample of retail cloth stores might not give us an accurate estimate of the total volume of sales, since a small number of establishments with a very large proportion of the total sales, may happen to get excluded from the sample.
In this case, one would be wise in stratifying the population of cloth stores in terms of some few cloth stores that have a very large volume of sales will constitute the uppermost stratum. The researcher would do well to include all of them in his sample.
That is, he may do well at times to take a 100% sample from this stratum and a much lesser percentage of cases from the other strata representing a large number of shops (with low or moderate volume of turn-over). Such a disproportionate sampling alone will most likely give reliable estimates in respect of the population.
Another reason for taking a larger proportion of cases from one stratum rather than from others is that the researcher may want to subdivide cases within each stratum for further analysis.
The sub-strata thus derived may not all contain enough number of cases to sample from and in the same proportion as the other sub-strata, hence would not afford enough cases to serve as an adequate basis for further analysis. This being the case, one may have to sample out higher proportion of cases from the sub-stratum.
In general terms, it may be said that greatest precision and representation can be obtained if samples from the various strata adequately reflect their relative variabilities with respect to characteristics under study rather than present their relative sizes in the ‘population.’
It is advisable to sample more heavily in strata where the researcher has a reason to believe that the variability about a given characteristic, e.g., attitudes or participation, would be greater.
Hence, in a study undertaken for predicting the outcome of the national elections employing the method of stratified sampling, with states as a basis of stratification, a heavier sample should be taken from the areas or regions where the outcome is severely clouded and greatly in doubt.
Type # 5. Disproportionate Stratified Sampling:
This same effect may well be achieved alternatively by drawing from each stratum an equal number of cases, regardless of how strongly or weakly the stratum is represented in the population.
As a corollary of the way it is selected, an advantage of disproportionate stratified sampling relates to the fact that all the strata are equally reliable from the point of view of the size of the sample. An even more important advantage is economy.
This type of sample is economical in that, the investigators are spared the troubles of securing an unnecessarily large volume of information from the most prevalent groups in the population.
Such a sample may, however, also betray the combined disadvantages of unequal number of cases, i.e., smallness and non-representativeness. Besides, a disproportionate sample requires deep knowledge of pertinent characteristics of the various strata.
Type # 6. Optimum Allocation Sample:
In this sampling procedure, the size of the sample drawn from each stratum is proportionate to both the size and the spread of values within any given stratum. A precise use of this sampling procedure involves the use of certain statistical concepts which have not yet been adequately or convincingly introduced.
We now know something about the stratified random sampling and its different manifestations. Let us now see how the variables or criteria for stratification should be planned.
The following considerations ideally enter into the selection of controls for stratification:
(a) The information germane to institution of strata should be up-to-date, accurate, complete, applicable to the population and available to the researcher.
Many characteristics of the population cannot be used as controls since no satisfactory statistics about them are available. In a highly dynamic society characterized by great upheavals in the population, the researcher employing the strategy of stratification typically runs the risk of going quite wrong in his estimates about the sizes of the strata he effects in his sample.
(b) The researcher should have reasons to believe that the factors or criteria used for stratification are significant in the light of the problem under study.
(c) Unless the stratum under consideration is large enough and hence the sampler and field workers have no great difficulty locating candidates for it, it should not be used.
(d) When selecting cases for stratification, the researcher should try to choose those that are homogeneous with respect to the characteristics that are significant for the problem under study. As was said earlier, stratification is effective to the extent that the elements within the stratum are like each other and at the same time different relative to the elements in other strata.
Let us now consider the merits and limitations of stratified random sampling in a general way:
(1) In employing the stratified random sampling procedure, the researcher can remain assured that no essential groups or categories will be excluded from the sample. Greater representativeness of the sample is thus assured and the occasional mishaps that occur in simple random sampling are thus avoided.
(2) In the case of more homogeneous populations, greater precision can be achieved with fewer cases.
(3) Compared to the simple random ones, stratified samples are more concentrated geographically, thereby reducing the costs in terms of time, money and energy in interviewing respondents.
(4) The samples that an interviewer chooses may be more representative if his quota is allocated by the impersonal procedure of stratification than if he is to use his own judgement (as in quota sampling).
The main limitation of stratified random sampling is that in order to secure the maximal benefits from it in the course of a study, the researcher needs to know a great deal about the problem of research and its relation to other factors. Such a knowledge is not always forthcoming and quite so often waiting is long.
It should be remembered that the viewpoint of the theory of probability sampling, it is essentially irrelevant whether stratification is introduced during the procedure of sampling or during the analysis of data, except in so far as the former makes it possible to control the size of the sample obtained from each stratum and thus to increase the efficiency of the sampling design.
In other words, the procedure of drawing a simple random sample and then dividing it into strata is equivalent in effect to drawing a stratified random sample using as the sampling frame within each stratum, the .population of that stratum which is included in the given simple random sample.
Type # 7. Cluster Sampling:
In the above types of sampling, the elements chosen in the sample may be so widely dispersed that interviewing them may entail heavy expenses, a greater proportion of non-productive time (spent during travelling), a greater likelihood of lack of uniformity among interviewers’ questionings, recordings and lastly, a heavy expenditure on supervising the field staff.
There are also other practical factors of that sampling. For example, it may be considered less objectionable and hence permissible to administer a questionnaire to three or four departments of a factory or office rather than administering it on a sample drawn from all the departments on a simple or stratified random basis, since this latter procedure may be much more disruptive of the factory routines.
It is for some of these reasons that large-scale survey studies seldom make use of simple or stratified random samples; instead, they make use of the method of cluster sampling.
In cluster sampling, the sampler first samples out from the population, certain large groupings, i.e., “cluster.” These clusters may be city wards, households, or several geographical or social units. The sampling of clusters from the population is done by simple or stratified random sampling methods. From these selected clusters, the constituent elements are sampled out by recourse to procedures ensuring randomness.
Suppose, for example, that a researcher wants to conduct a sample study on the problems of undergraduate students of colleges in Maharashtra.
He may proceed as follows:
(a) First he prepares a list of all the universities in the state and selects a sample of the universities on a ‘random’ basis.
(b) For each of the universities of the state included in the sample, he makes a list of colleges under its jurisdiction and takes a sample of colleges on a ‘random’ basis.
(c) For each of the colleges that happen to get included in the sample, he makes a list of all undergraduate students enrolled with it. From out of these students, he selects a sample of the desired size on a ‘random’ basis (simple or stratified).
In this manner, the researcher gets a probability or random sample of elements, more or less concentrated, geographically. This way he is able to avoid heavy expenditure that would otherwise have been incurred had he resorted to simple or stratified random sampling, and yet he need not sacrifice the principles and benefits of probability sampling.
Characteristically, this sampling procedure moves through a series of stages. Hence it is, in a sense, a ‘multi-stage’ sampling and sometimes known by this name. This sampling procedure moves progressively from the more inclusive to the less inclusive sampling units the researcher finally arrives at those elements of population that constitute his desired sample.
It should be noted that with cluster sampling, it is no longer true that every combination of the desired number of elements in the population is equally likely to be selected as the sample of the population. Hence, the kind of effects that we saw in our analysis of simple random samples, i.e., the population-value being the most probable sample-value, cannot be seen here.
But such effects do materialize in a more complicated way, though, of course, the sampling efficiency is hampered to some extent. It has been found that on a per case basis, the cluster sampling is much less efficient in getting information than comparably effective stratified random sampling.
Relatively speaking, in the cluster sampling, the margin of error is much greater. This handicap, however, is more than balanced by associated economies, which permit the sampling of a sufficiently large number of cases at a smaller total cost.
Depending on the specific features of the sampling plan attendant upon the objects of survey, cluster sampling may be more or less efficient than simple random sampling. The economies associated with cluster sampling generally tilt the balance in favour of employing cluster sampling in large-scale surveys, although compared to simple random sampling, more cases are needed for the same level of accuracy.
Type # 8. Multi-Phase Sampling:
It is sometimes convenient to confine certain questions about specific aspects of the study to a fraction of the sample, while other information is being collected from the whole sample. This procedure is known as ‘multi-phase sampling.’
The basic information recorded from the whole sample makes it possible to compare certain characteristics of the sub-sample with that of the whole sample.
One additional point that merits mention is that multi-phase sampling facilitates stratification of the sub-sample since the information collected from the first phase sample can sometimes be gathered before the sub-sampling process takes place. It will be remembered that panel studies involve multi-phase sampling.
DIFFERENCE BETWEEN CENSUS AND SAMPLING
Difference between Census and Sampling
Census and sampling are two methods of collecting survey data about the population that are used by many countries. Census refers to the quantitative research method, in which all the members of the population are enumerated. On the other hand, the sampling is the widely used method, in statistical testing, wherein a data set is selected from the large population, which represents the entire group
.
Census implies complete enumeration of the study objects, whereas Sampling connotes enumeration of the subgroup of elements chosen for participation. These two survey methods are often contrasted with each other, and so this article makes an attempt to clear the differences between census and sampling, in detail; Have a look.
BASIS FOR COMPARISON | CENSUS | SAMPLING |
Meaning | A systematic method that collects and records the data about the members of the population is called Census. | Sampling refers to a portion of the population selected to represent the entire group, in all its characteristics. |
Enumeration | Complete | Partial |
Study of | Each and every unit of the population. | Only a handful of units of the population. |
Time required | It is a time consuming process. | It is a fast process. |
Cost | Expensive method | Economical method |
Results | Reliable and accurate | Less reliable and accurate, due to the margin of error in the data collected. |
Error | Not present. | Depends on the size of the population |
Appropriate for | Population of heterogeneous nature. | Population of homogeneous nature. |
SAMPLING
Sampling is a process used in statistical analysis in which a predetermined number of observations are taken from a larger population. The methodology used to sample from a larger population depends on the type of analysis being performed but may include simple random sampling or systematic sampling.
In business, a CPA performing an audit uses sampling to determine the accuracy of account balances in the financial statements, and managers use sampling to assess the success of the firm’s marketing efforts.
The sample should be a representation of the entire population. When taking a sample from a larger population, it is important to consider how the sample is chosen. To get a representative sample, the sample must be drawn randomly and encompass the whole population. For example, a lottery system could be used to determine the average age of students in a university by sampling 10% of the student body.
Examples of Sample Tests for Marketing
Businesses aim to sell their products and/or services to target markets. Before presenting products to the market, companies generally identify the needs and wants of their target audience. To do so, they may employ using a sample of the population to gain a better understanding of those needs to later create a product and/or service that meets those needs. Gathering the opinions of the sample helps to identify the needs of the whole.
What is Non-Probability Sampling?
Non-probability sampling is a sampling technique where the odds of any member being selected for a sample cannot be calculated. It’s the opposite of probability sampling, where you can calculate the odds. In addition, probability sampling involves random selection, while non-probability sampling does not–it relies on the subjective judgement of the researcher.
The odds do not have to be equal for a method to be considered probability sampling. For example, one person could have a 10% chance of being selected and another person could have a 50% chance of being selected. It’s non-probability sampling when you can’t calculate the odds at all.
Types of Non-Probability Sampling
Types of Non-Probability Sampling
· Convenience Sampling: as the name suggests, this involves collecting a sample from somewhere convenient to you: the mall, your local school, your church. Sometimes called accidental sampling, opportunity sampling or grab sampling.
· Haphazard Sampling: where a researcher chooses items haphazardly, trying to simulate randomness. However, the result may not be random at all and is often tainted by selection bias.
· Purposive Sampling: where the researcher chooses a sample based on their knowledge about the population and the study itself. The study participants are chosen based on the study’s purpose. There are several types of purposive sampling. For a full list, advantages and disadvantages of the method, see the article: Purposive Sampling.
· Expert Sampling: in this method, the researcher draws the sample from a list of experts in the field.
· Heterogeneity Sampling / Diversity Sampling: a type of sampling where you deliberately choose members so that all views are represented. However, those views may or may not be represented proportionally.
· Modal Instance Sampling: The most “typical” members are chosen from a set.
· Quota Sampling: where the groups (i.e. men and women) in the sample are proportional to the groups in the population.
· Snowball Sampling: where research participants recruit other members for the study. This method is particularly useful when participants might be hard to find. For example, a study on working prostitutes or current heroin users.
How to Develop a Good Research Question:
· Researchers should begin by identifying a broader subject of interest that lends itself to investigation. For example, a researcher may be interested in childhood obesity.
· The next step is to do preliminary research on the general topic to find out what research has already been done and what literature already exists. How much research has been done on childhood obesity? What types of studies? Is there a unique area that yet to be investigated or is there a particular question that may be worth replicating?
· Then begin to narrow the topic by asking open-ended "how" and "why" questions. For example, a researcher may want to consider the factors that are contributing to childhood obesity or the success rate of intervention programs. Create a list of potential questions for consideration and choose one that interests you and provides an opportunity for exploration.
· Finally, evaluate the question by using the following list of guidelines:
· Is the research question one that is of interest to the researcher and potentially to others? Is it a new issue or problem that needs to be solved or is it attempting to shed light on previously researched topic.
· Is the research question researchable? Consider the available time frame and the required resources. Is the methodology to conduct the research feasible?
· Is the research question measureable and will the process produce data that can be supported or contradicted?
· Is the research question too broad or too narrow?
Types of sampling design in Research Methodology
There are different types of sample designs based on two factors viz., the representation basis and the element selection technique. On the representation basis, the sample may be probability sampling or it may be non-probability sampling. Probability sampling is based on the concept of random selection, whereas non-probability sampling is ‘non-random’ sampling. On element selection basis, the sample may be either unrestricted or restricted. When each sample element is drawn individually from the population at large, then the sample so drawn is known as ‘unrestricted sample’, whereas all other forms of sampling are covered under the term ‘restricted sampling’. The following chart exhibits the sample designs as explained above.
Thus, sample designs are basically of two types viz., non-probability sampling and probability sampling. We take up these two designs separately.
Non-probability sampling: Non-probability sampling is that sampling procedure which does not afford any basis for estimating the probability that each item in the population has of being included in the sample. Non-probability sampling is also known by different names such as deliberate sampling, purposive sampling and judgement sampling. In this type of sampling, items for the sample are selected deliberately by the researcher; his choice concerning the items remains supreme. In other words, under non-probability sampling the organizers of the inquiry purposively choose the particular units of the universe for constituting a sample on the basis that the small mass that they so select out of a huge one will be typical or representative of the whole. For instance, if economic conditions of people living in a state are to be studied, a few towns and villages may be purposively selected for intensive study on the principle that they can be representative of the entire state. Thus, the judgement of the organizers of the study plays an important part in this sampling design.
Probability sampling: Probability sampling is also known as ‘random sampling’ or ‘chance sampling’. Under this sampling design, every item of the universe has an equal chance of inclusion in the sample. It is, so to say, a lottery method in which individual units are picked up from the whole group not deliberately but by some mechanical process. Here it is blind chance alone that determines whether one item or the other is selected. The results obtained from probability or random sampling can be assured in terms of probability i.e., we can measure the errors of estimation or the significance of results obtained from a random sample, and this fact brings out the superiority of random sampling design over the deliberate sampling design. Random sampling ensures the law of Statistical Regularity which states that if on an average the sample chosen is a random one, the sample will have the same composition and characteristics as the universe. This is the reason why random sampling is considered as the best technique of selecting a representative sample. In such a design, personal element has a great chance of entering into the selection of the sample. The investigator may select a sample which shall yield results favorable to his point of view and if that happens, the entire inquiry may get vitiated. Thus, there is always the danger of bias entering into this type of sampling technique. But in the investigators are impartial, work without bias and have the necessary experience so as to take sound judgment, the results obtained from an analysis of deliberately selected sample may be tolerably reliable. However, in such a sampling, there is no assurance that every element has some specifiable chance of being included. Sampling error in this type of sampling cannot be estimated and the element of bias, great or small, is always there. As such this sampling design in rarely adopted in large inquires of importance. However, in small inquiries and researches by individuals, this design may be adopted because of the relative advantage of time and money inherent in this method of sampling. Quota sampling is also an example of non-probability sampling. Under quota sampling the interviewers are simply given quotas to be filled from the different strata, with some restrictions on how they are to be filled. In other words, the actual selection of the items for the sample is left to the interviewer’s discretion. This type of sampling is very convenient and is relatively inexpensive. But the samples so selected certainly do not possess the characteristic of random samples. Quota samples are essentially judgement samples and inferences drawn on their basis are not amenable to statistical treatment in a formal way.
What is Sample design in Research Methodology ?
A sample design is made up of two elements. Random sampling from a finite population refers to that method of sample selection which gives each possible sample combination an equal probability of being picked up and each item in the entire population to have an equal chance of being included in the sample. This applies to sampling without replacement i.e., once an item is selected for the sample, it cannot appear in the sample again (Sampling with replacement is used less frequently in which procedure the element selected for the sample is returned to the population before the next element is selected. In such a situation the same element could appear twice in the same sample before the second element is chosen). In brief, the implications of random sampling (or simple random sampling) are:
· It gives each element in the population an equal probability of getting into the sample; and all choices are independent of one another.
· It gives each possible sample combination an equal probability of being chosen.
Keeping this in view we can define a simple random sample (or simply a random sample) from a finite population as a sample which is chosen in such a way that each of the NCn possible samples has the same probability, 1/NCn, of being selected. To make it more clear we take a certain finite population consisting of six elements (say a, b, c, d, e, f ) i.e., N = 6. Suppose that we want to take a sample of size n = 3 from it. Then there are 6C3 = 20 possible distinct samples of the required size, and they consist of the elements abc, abd, abe, abf, acd, ace, acf, ade, adf, aef, bcd, bce, bcf, bde, bdf, bef, cde, cdf, cef, and def. If we choose one of these samples in such a way that each has the probability 1/20 of being chosen, we will then call this a random sample.
Nature of management
Nature if management: Management is a universal activity in nature as every organization requires making of decision, procurement of resour...
Popular Posts
-
8 Important Types of Probability Sampling The eight important types of probability sampling used for conducting social research. The types...
-
VALUES According to M. Haralambos (2000), “A value is a belief that something is good and desirable.” FEATURES/CHARACTERISTICS OF VALUES Val...
-
Introduction to research process Writers usually treat the research task as a sequential process involving several clearly defined s...